向量点乘叉乘

向量点乘

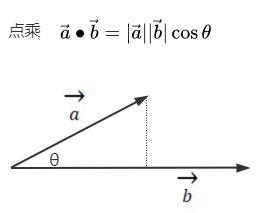
几何含义

点乘结果：向量a长度 * 向量b长度 * cos(ab夹角);

const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);
// dot几何含义：向量a长度 * 向量b长度 * cos(ab夹角)
const dot = a.dot(b);

单位向量点乘

返回结果就是夹角 θ 的余弦值cos(θ)

const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);
// a、b向量归一化后点乘
const cos = a.clone().normalize().dot(b.clone().normalize());
console.log("向量夹角余弦值", cos);

夹角余弦值转角度值

//反余弦计算向量夹角弧度
const rad = Math.acos(cos);
// 弧度转角度
const angle = THREE.MathUtils.radToDeg(rad);

向量叉乘

语法

• crossVectors

  // 创建一个向量c，用来保存叉乘结果
  const c = new THREE.Vector3();
  //向量a叉乘b，结果保存在向量c
  c.crossVectors(a, b);

• cross

  const c = new THREE.Vector3();
  c.crossVectors(a, b);
  const c = a.clone().cross(b);

叉乘结果几何含义

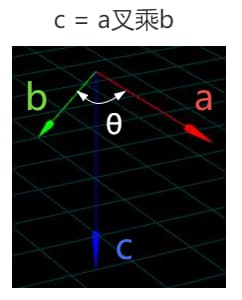
• 向量 a 叉乘向量 b，得到一个新的向量 c, 向量 c 同时垂直于向量 a、向量 b
• 向量 c 的长度 c.length() = a.length()*b.length()*sin(θ)

箭头可视化向量

//给箭头设置一个起点(随便给个位置就行)
const O = new THREE.Vector3(0, 0, 0);
// 红色箭头表示向量a
const arrowA = new THREE.ArrowHelper(a.clone().normalize(), O, a.length(), 0xff0000);
// 绿色箭头表示向量b
const arrowB = new THREE.ArrowHelper(b.clone().normalize(), O, b.length(), 0x00ff00);

叉乘不满足交换律

叉乘顺序不同结果也不同

// a叉乘b
c.crossVectors(a, b);
// b叉乘a
c.crossVectors(b, a);

叉乘计算三角形面积

两个向量叉乘结果：a.length()*b.length()*sin(θ)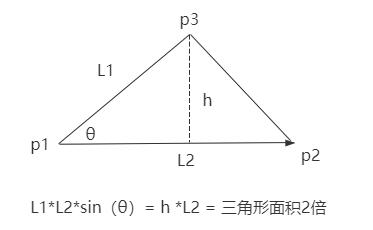 投射到三角形上h = L1*sinθ, 所以L1 * L2 x sinθ= h x L2 = 三角形面积2倍

由此可以计算:

// 三角形两条边构建两个向量
const a = p2.clone().sub(p1);
const b = p3.clone().sub(p1);
// 两个向量叉乘结果c的几何含义：a.length()*b.length()*sin(θ)
const c = a.clone().cross(b);

// 三角形面积计算
const S = 0.5 * c.length();